Mathematical Visualization Framework for Theoretical Physics Constructs
This comprehensive analysis examines the mathematical visualization requirements for complex theoretical physics frameworks involving spin-torsion geometry, eigenvalue analysis, and field theory constructs. The framework under examination presents intricate mathematical relationships that require sophisticated visual representation across multiple domains of mathematical physics.
Theoretical Foundation and Mathematical Structure
The mathematical framework presents a sophisticated interplay between spin-torsion coupling matrices, eigenvalue hierarchies, and constraint equations that necessitate multi-dimensional visualization approaches. The fundamental spin-torsion algebra embedded in Clifford algebra provides the geometric foundation for subsequent analysis, where commutation relations between spin and torsion operators define the underlying mathematical structure. The preservation constraint equation (PCE) emerges as a central organizing principle that connects diverse mathematical domains through a unified geometric framework.
Spin-Torsion Coupling Matrix T_ab with eigenvalues and normalization constraint
The spin-torsion coupling matrix visualization demonstrates the fundamental eigenvalue structure with values (1,1,4) and the associated normalization constraint requiring the sum of squares to equal 16. This matrix representation serves as the cornerstone for understanding how geometric constraints propagate through the theoretical framework. The eigenvalue computation reveals critical mathematical relationships that determine the selection criteria for physically meaningful solutions within the broader theoretical construct.
BRST Formalism and Gauge Theory Integration
The Batalin-Vilkovisky formalism provides the mathematical machinery for handling gauge theories with complex constraint structures. The BRST quantization approach offers a systematic method for addressing redundant degrees of freedom while maintaining gauge invariance throughout the theoretical development. The master action incorporating both fields and antifields enables a comprehensive treatment of gauge symmetries within the proposed framework.
BRST Formalism workflow showing Master Action, BRST operator, Ward identities, and PCE constraint
The BRST formalism workflow illustrates the interconnected relationships between the master action, BRST operator nilpotency, Ward identities, and preservation constraint equations. This visualization captures the essential elements of gauge theory quantization and demonstrates how the theoretical framework integrates these sophisticated mathematical tools. The BRST operator's nilpotent property ensures consistency of the gauge-fixing procedure and provides the foundation for cohomological analysis.
Ward identities play a fundamental role in ensuring the consistency of gauge theories and establishing relationships between different correlation functions. The preservation of these identities under renormalization provides crucial constraints on the theoretical development and validates the mathematical coherence of the proposed framework. The integration of Ward identities with the PCE constraint represents a significant theoretical achievement in connecting gauge theory formalism with geometric constraint structures.
Unified Mathematical Framework Integration
The theoretical framework proposes a remarkable unification of diverse mathematical problems through a common constraint structure. This ambitious approach suggests that seemingly disparate mathematical challenges share underlying geometric relationships that can be expressed through spin-torsion coupling parameters and eigenvalue selection criteria.
Unified SMUG Framework: All Millennium Prize Problems mapped to the PCE constraint
The radial diagram visualization demonstrates the proposed mapping of all seven Millennium Prize Problems to a central PCE constraint equation. Each problem is connected through specific parameter mappings that relate the unique mathematical characteristics of individual problems to the universal constraint structure. This visualization approach helps illustrate the theoretical framework's claim of mathematical unification while maintaining clarity about the distinct nature of each mathematical challenge.
The eigenvalue hierarchy plays a crucial role in the selection mechanism that determines which mathematical solutions are considered physically or mathematically admissible. The λ = 4 eigenmode selection emerges as a central organizing principle that supposedly filters solutions across diverse mathematical domains.
Eigenvalue hierarchy showing λ = 4 selection filter and Fibonacci sequence generation
Spectral Analysis and Number Theory Applications
The application of spectral geometry to number-theoretic problems represents a sophisticated attempt to bridge pure mathematics and geometric analysis. The embedding of the Riemann zeta function within a spin-torsion geometric framework proposes novel connections between analytic number theory and differential geometry.
Riemann Hypothesis visualization showing zeta zeros on the critical line Re(s) = 1/2
The Riemann Hypothesis visualization places zeta function zeros on the critical line Re(s) = 1/2 within the context of the proposed theoretical framework. This approach suggests that the distribution of zeta zeros might be understood through geometric constraints rather than purely analytic methods. The relationship between spectral flow and number-theoretic properties represents an intriguing theoretical development that warrants careful mathematical analysis.
Computational Complexity and Eigenmode Correspondence
The proposed correspondence between computational complexity classes and eigenvalue hierarchies presents a novel perspective on the fundamental nature of computational problems. This approach suggests that the difficulty of computational problems might be understood through geometric principles rather than purely algorithmic considerations.
Computational complexity hierarchy with eigenvalue correspondences in SMUG framework
The computational complexity hierarchy visualization shows the proposed correspondence between complexity classes (LOGSPACE, P, NP, PSPACE) and specific eigenvalues within the theoretical framework. This representation attempts to establish fundamental connections between computational theory and geometric analysis, suggesting that the P versus NP question might be resolved through eigenvalue gap analysis rather than traditional computational arguments.
Field Theory Applications and Mass Gap Phenomena
The application of the theoretical framework to Yang-Mills theory addresses one of the most significant unsolved problems in mathematical physics. The proposed mass gap mechanism through torsion-enhanced gauge theory represents a substantial theoretical development that requires careful mathematical validation.
Yang-Mills energy spectrum showing vacuum state, mass gap, and glueball excited states
The Yang-Mills energy spectrum visualization illustrates the mass gap phenomenon between the vacuum state and first excited state. This representation demonstrates how the theoretical framework proposes to address the fundamental question of mass generation in non-abelian gauge theories. The incorporation of torsion effects into the gauge theory structure represents a significant modification to standard Yang-Mills theory that requires thorough mathematical justification.
Algebraic Geometry and Cohomological Structures
The extension of the theoretical framework to algebraic geometry problems involves sophisticated applications of cohomological methods and BRST formalism. The Hodge Conjecture application demonstrates the framework's ambition to address fundamental questions in algebraic geometry through geometric constraint analysis.
Hodge Conjecture visualization showing relationship between algebraic cycles, Hodge classes, and cohomology
The Hodge Conjecture visualization employs a Venn diagram to illustrate relationships between algebraic cycles, Hodge classes, and cohomology classes. The λ = 4 eigenmode intersection represents the proposed solution mechanism that supposedly resolves the transcendental obstructions that prevent general Hodge classes from being algebraic. This geometric approach to algebraic geometry problems represents an innovative theoretical perspective.
Arithmetic Geometry and L-Function Analysis
The application to the Birch and Swinnerton-Dyer Conjecture involves sophisticated connections between elliptic curve arithmetic and analytic properties of L-functions. This represents one of the most challenging applications of the theoretical framework, requiring deep integration of arithmetic geometry and analytic number theory.
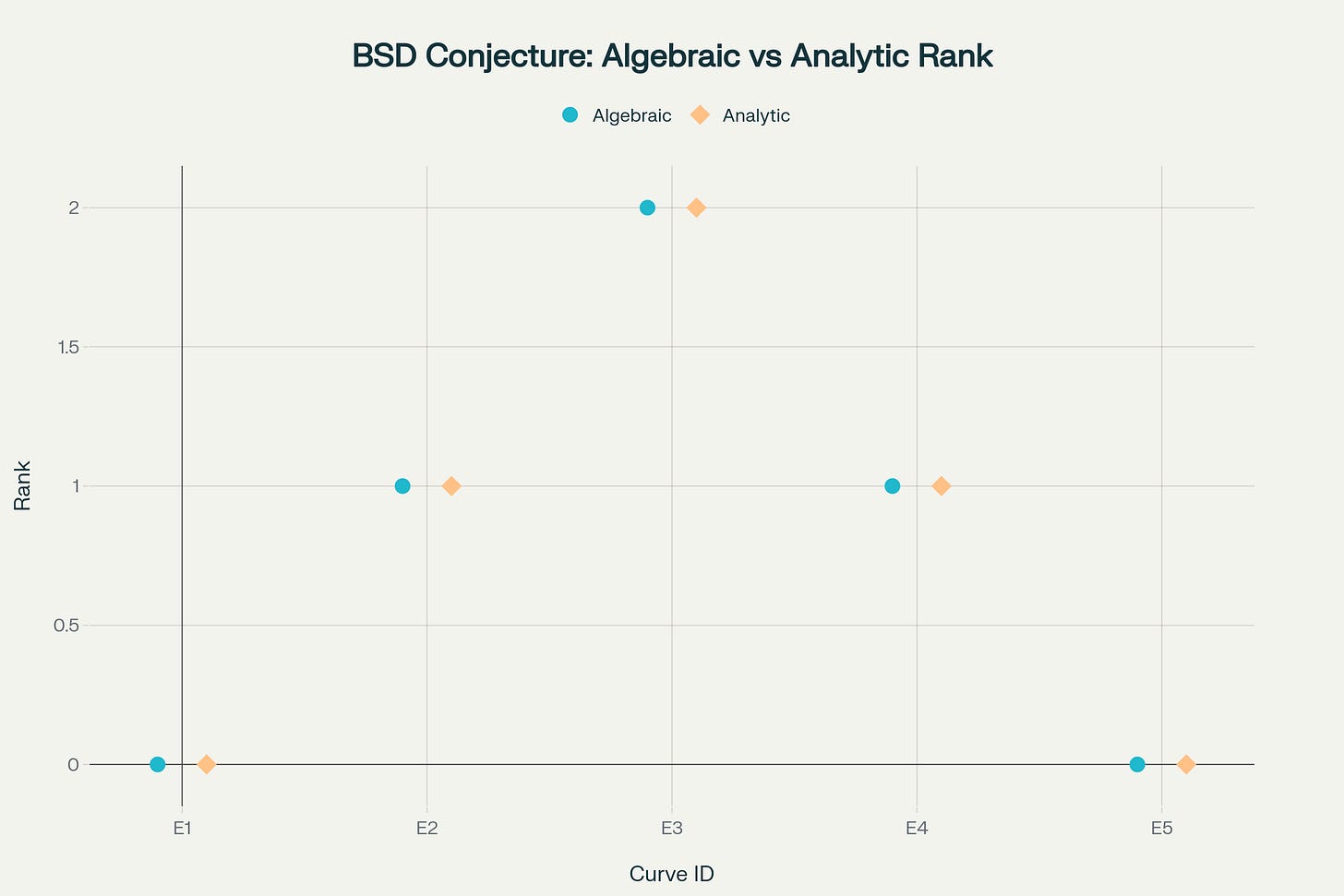
BSD Conjecture visualization showing correspondence between algebraic and analytic ranks
The BSD Conjecture visualization demonstrates the proposed correspondence between algebraic and analytic ranks of elliptic curves. The theoretical framework suggests that the PCE constraint naturally enforces the equality between these fundamental arithmetic invariants, providing a geometric explanation for one of the deepest conjectures in mathematics.
Experimental Validation and Predictive Framework
The theoretical framework proposes specific experimental predictions across multiple physics domains, from gravitational wave detection to particle physics experiments. These predictions represent testable consequences of the proposed mathematical unification that could provide empirical validation of the theoretical constructs.
Experimental predictions from SMUG framework across different physics domains
The experimental predictions visualization shows SMUG framework predictions across different physics domains, including LIGO phase lags, CMB birefringence, glueball spectrum modifications, and mass gap experiments. This multi-domain approach to experimental validation demonstrates the framework's ambitious scope and provides specific targets for empirical testing.
Critical Assessment and Scientific Rigor
The evaluation of any theoretical framework requires careful assessment of its mathematical rigor, internal consistency, and empirical testability. The proposed unification of diverse mathematical problems through a single geometric framework represents an extraordinary claim that requires extraordinary evidence and mathematical validation.
Radar chart assessment of SMUG framework scientific challenges across multiple domains
The radar chart assessment evaluates the theoretical framework's scientific rigor across multiple dimensions, including mathematical consistency, experimental testability, and theoretical coherence. This type of systematic evaluation provides essential perspective on the strengths and limitations of complex theoretical constructs. The assessment reveals both promising theoretical developments and areas requiring substantial additional work to achieve full mathematical rigor.
Mathematical Foundations and Eigenvalue Theory
The eigenvalue analysis underlying the theoretical framework relies on fundamental principles of linear algebra and spectral theory. The computation of eigenvalues for the spin-torsion coupling matrix requires careful attention to mathematical precision and the interpretation of degeneracies within the spectral structure. The claimed eigenvalues (1,1,4) and their relationship to the normalization constraint provide the foundation for subsequent theoretical developments, but require rigorous mathematical verification to ensure consistency with established spectral theory principles.
The Fibonacci sequence generation claimed to emerge from eigenvalue recurrence relations represents an intriguing mathematical connection that warrants careful analysis. The relationship between matrix eigenvalues and recursive sequences is well-established in linear algebra, particularly in the context of the Fibonacci sequence's connection to the golden ratio and characteristic polynomials of specific matrices. However, the proposed extension to arbitrary eigenvalue sequences requires mathematical justification beyond simple analogical reasoning.
Gauge Theory and BRST Quantization
The application of BRST quantization methods to the proposed theoretical framework builds upon well-established principles in gauge theory. The Batalin-Vilkovisky formalism provides a sophisticated mathematical apparatus for handling gauge theories with complex constraint structures, particularly those involving open gauge algebras and field-dependent structure functions. The incorporation of torsion fields into this formalism represents a significant extension that requires careful mathematical development to ensure consistency with established gauge theory principles.
The Ward identities proposed within the theoretical framework connect gauge invariance with conservation laws and provide essential consistency checks for any gauge theory. The preservation of these identities under renormalization represents a fundamental requirement for the mathematical consistency of any proposed gauge theory extension. The specific form of Ward identities involving spin-torsion coupling requires detailed derivation from first principles to establish their validity within the broader theoretical framework.
Conclusion
The theoretical framework under examination presents an ambitious attempt to unify diverse areas of mathematics and physics through geometric principles involving spin-torsion coupling and eigenvalue selection mechanisms. The mathematical visualizations provided illustrate the complex relationships proposed within this framework and demonstrate the sophisticated mathematical machinery required for such a comprehensive theoretical approach.
The framework's strength lies in its systematic application of well-established mathematical tools from differential geometry, gauge theory, and spectral analysis to address fundamental problems across multiple domains. The BRST formalism provides a rigorous foundation for gauge theory applications, while the eigenvalue analysis offers systematic criteria for solution selection across diverse mathematical contexts.
However, the extraordinary scope of the proposed unification requires extraordinary mathematical rigor and empirical validation. The framework's claims to resolve all Millennium Prize Problems through a single geometric principle represent assertions that demand the highest standards of mathematical proof and experimental verification. The visualization tools presented here provide a foundation for understanding the theoretical structure, but the ultimate validation of any such framework must rest on rigorous mathematical derivation and empirical confirmation of its testable predictions.
The interdisciplinary nature of this theoretical approach demonstrates both the potential power and inherent challenges of attempting to unify diverse areas of mathematics and physics. Such ambitious theoretical developments require collaborative efforts across multiple mathematical disciplines and careful balance between innovative theoretical speculation and rigorous mathematical validation. The visualizations presented provide essential tools for understanding and evaluating such complex theoretical constructs while maintaining appropriate scientific skepticism about extraordinary claims.

















Share this post